Classificação das Superfícies.


Superfícies reais.

Exemplos básicos de superfícies reais: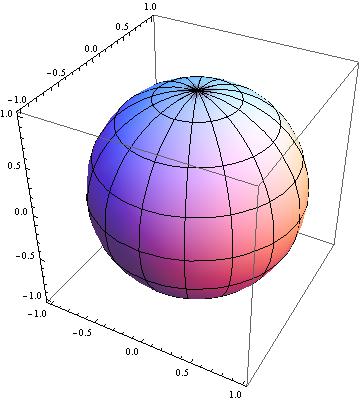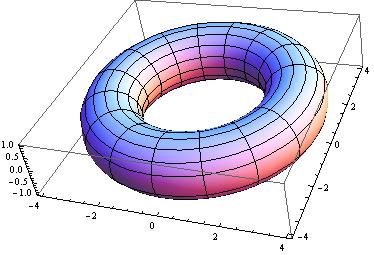


  • Esfera (S2):
  • Toro (T):
  • n Toro (nT):
    • Fig.1 Esfera Fig.2 ToroFig.3 2-Toro



    Tipos de superfícies:
    As superfícies reais podem ser separadas em dois grupos distintos: superfícies orientáveis e não-orientáveis. As superfícies orientáveis são aquelas que possuem duas faces, a face que se localiza no interior e a face que se localiza no exterior, tal como a esfera S2 e o Toro. As superfícies não-orientáveis não possuem essa distinção de faces, pois contém a faixa de Möbius, onde a face externa e interna é a mesma, como o RP2 e a garrafa de Klein.
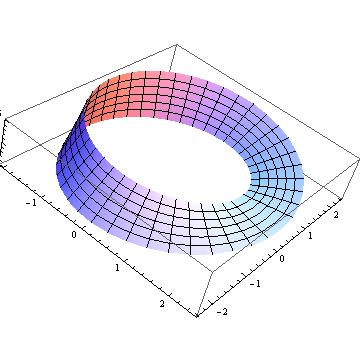    Fig.4 Faixa de Möbius



    À partir de S2, T e RP2 é possível obter-se toda superfície real compacta conexa através de somas conexas, onde o operador desta função é representado por #:
  • T # S2 = T, pois a esfera representa identidade em somas conexas.
  • T # T = 2T
  • Y # S2 = Y, para qualquer superfície real Y.
  • RP2 # RP2 = Garrafa de Klein.


    • Representação com polígonos


    Professora Orientadora: Elizabeth Gasparim

    Aluno: José Marcelo Maizman Bogdan